Fake news sobre o Número de Ouro

Will
12/02/2019
1

tirinha número de ouro razão áurea retângulo de ouro

Se você nunca ouviu falar no número de ouro, não se preocupe, ele não passa de um número como outro qualquer.

Eita! Esse post promete.

Deixando a “zuera” de lado, vou tentar explicar rapidamente o que é o número de ouro, usando outro número conhecido como exemplo.

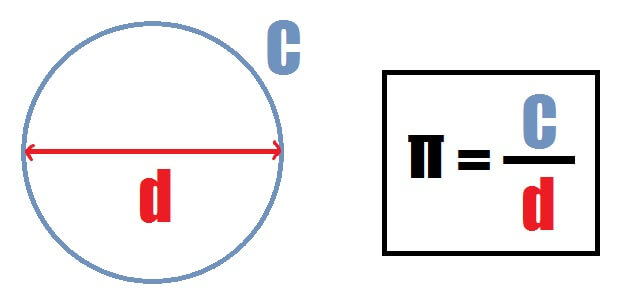
Você já ouviu falar no número “Pi”, aquele representado pela letra grega π? Do valor 3,14159… lembra? Não?!

Então, para QUALQUER circunferência, toda vez que a gente divide a medida do comprimento dela pela medida do diâmetro dela, a gente encontra o Pi. Assim, oh!

Espero que tenha lembrado. ¬¬

Vale ressaltar também que existem muitos outros modos de achar o valor de π , mas não vou mostrar aqui, tá?

– Beleza, mas e o número de ouro?

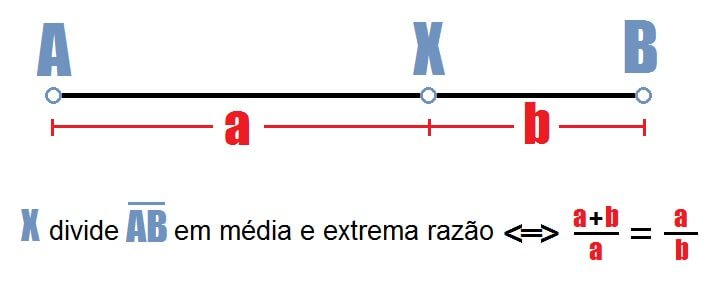
O número de ouro, representado pela letra grega “Fi”, ϕ (maiúsculo) ou φ (minúsculo), aparece quando a gente divide um segmento qualquer de um jeito especial. Por exemplo, usando a figura abaixo como referência, é só cortar o segmento $\overline{\mathrm{AB}}$ num ponto X de tal forma que o segmento todo $\overline{\mathrm{AB}}$ esteja para o segmento $\overline{\mathrm{AX}}$ , assim como $\overline{\mathrm{AX}}$ está para o segmento menor $\overline{\mathrm{XB}}$ .

$\frac {\mathrm{AB}} {\mathrm{AX}} = \frac {\mathrm{AX}} {\mathrm{XB}}$

Calma! Parece complicado, mas com a figura a seguir e um pouco de força de vontade da sua parte dá pra entender. Oia aí.

seção áurea divisão em média e extrema razão

Só pra reforçar, ${\mathrm{AB}} = \mathrm{a+b}$ , ${\mathrm{AX}} = \mathrm{a}$ , ${\mathrm{XB}} = \mathrm{b}$ . E se quiser conferir como desenvolver a equação da imagem acima, é só clicar aqui. O professor Rafael Procópio mostra todas contas passo a passo. Ui!

No vídeo “Fake news sobre o número de ouro“, que você com certeza vai ver logo mais à frente, a gente usou outras letras e um segmento de reta de tamanho 1. Desse jeito, na minha opinião, fica mais fácil de fazer toda manipulação algébrica e o valor do φ sai direto.

E só para você não ficar maluco, ao longo do post, vou falar sobre o número de ouro e vou usar outros nomes que estão intimamente ligados a ele, por exemplo: razão áurea, seção áurea, proporção divina, retângulo áureo, espiral áurea etc. Esses termos não são sinônimos do número de ouro, mas têm alguma ligação com ele, beleza?

Só pra você saber, no mundo acadêmico, em grandes sites de educação, em livros didáticos e em vídeos famosos, como por exemplo o “Donald no país da Matemágica“, é comum ouvir falar que o número de ouro está relacionado diretamente à estética e à beleza, está presente na natureza, na arquitetura, na música, nas pinturas, no corpo humano, no cartão de crédito e por aí vai. A lista é bem grande inclusive.

E, já que citei o cartão de crédito, antes de começar a falar dos outros pontos, vou mostrar ibagens.

Será que os cartões de crédito e débito possuem o número de ouro? Se dividirmos a medida do lado maior pela medida do lado menor, encontraremos um valor próximo de 1,618?

cartão de crédito débito razão áurea número de ouro

De acordo com o ISO 7810, as medidas do cartão devem ser 85,60 mm x 53,98 mm.

– Olha a precisão, duas casas depois da vírgula! =O

Pois é, mas e daí? Podemos considerar que o número de ouro está presente no cartão de crédito?

Bom, eu fiz a divisão aqui de 85,60 mm por 53,98 mm e obtive 1,585… Mesmo com uma diferença pequena de ± 0,03 mm, eu tendo a NÃO acreditar. Digo isso porque, se (por hipótese) o objetivo era definir um tamanho de cartão que tivesse a razão áurea, por que não escolheram 85 mm x 52,5 mm? Olha aí, medidas quase redondas e se fizermos a divisão da maior pela menor vamos obter ~1,619. =)

Pode ser que exista uma questão técnica por trás da confecção dos cartões e inviabilize a construção com as medidas que citei. De qualquer forma, basta o pessoal da Organização Internacional da Normalização (ISO) dizer que usam a razão áurea de propósito. ISO ajudaria bastante. 😉

Deixando o cartão de crédito de lado, será que o número de ouro está presente na natureza, na arquitetura, na música, nas pinturas, no corpo humano e está diretamente relacionado à estética e à beleza?

Já te digo de antemão que nem tudo que reluz é ouro.

No vídeo a seguir, a gente traz informações sobre o número de ouro e comenta se existe alguma relação dele com a questão estética, com a Monalisa de Leonardo da Vinci, com o edifício grego Partenon e muito mais. Assiste aí, está bem legal. Se não quiser assistir pela Matemática, que seja pelos efeitos especiais. 😉

Como você viu, descobrimos que várias informações que rolam por aí sobre o número de ouro não têm comprovação científica, não têm evidências. Sem contar que essa história do retângulo áureo ser o mais bonito é pura balela. Ah, e ainda existem mais fake news sobre o número de ouro, viu?

Vou colocar aqui mais alguns equívocos que a gente não falou no vídeo, mas que foram levantados pelo Professor George Markowsky, no artigo Equívocos sobre a razão áurea:

Acreditar que a pirâmide de Quéops, lá no Egito, foi construída seguindo proporções áureas.
Achar que o Edifício do Secretariado das Nações Unidas em Nova Iorque nos Estados Unidos possui proporções áureas.
Achar que o corpo humano exibe proporções áureas.

Só para complementar o equívoco relacionado à pirâmide citado pelo professor George, no capítulo 3 do livro Razão áurea – A história de Fi, um número surpreendente, do autor Mario Livio, há bastante informação sobre a relação entre o número de ouro e a grande pirâmide. Inclusive, recomendamos a leitura do livro inteiro. hehehe 😉 O capítulo termina da seguinte forma:

[…]Contudo, alguns egiptólogos afirmam que existe de fato evidência direta sugerindo que nem a Razão Áurea nem Pi foram usados no projeto da Grande pirâmide (nem mesmo involuntariamente).

[…]Será que está encerrado, então, o caso de 4.500 anos de Razão Áurea e da Grande pirâmide? Certamente, esperaríamos que sim, mas, infelizmente, a história mostrou que o apelo místico das pirâmides e o Numerismo Áureo podem ser mais fortes do que qualquer evidência sólida. Os argumentos apresentados por Petrie, Gillings, Mendelssohn e Herz-Fischler estão disponíveis há décadas, mas isto não impediu a publicação de muitos livros que repetiam a falácia da Razão Áurea.

Para nosso objetivo, temos de concluir que é bastante improvável que os antigos babilônios ou os antigos egípcios tenham descoberto a Razão Áurea e suas propriedades. Esta tarefa foi deixada para os matemáticos gregos.
LIVIO, 2008, p.57

Interessante, né?

Já para o caso do corpo humano exibir proporções áureas, em geral, quando se fala sobre esse assunto, é comum usar como exemplo aquela imagem famosa do estudo do Leonardo da Vinci, O Homem Vitruviano. Será que o número de ouro está presente nessa obra?

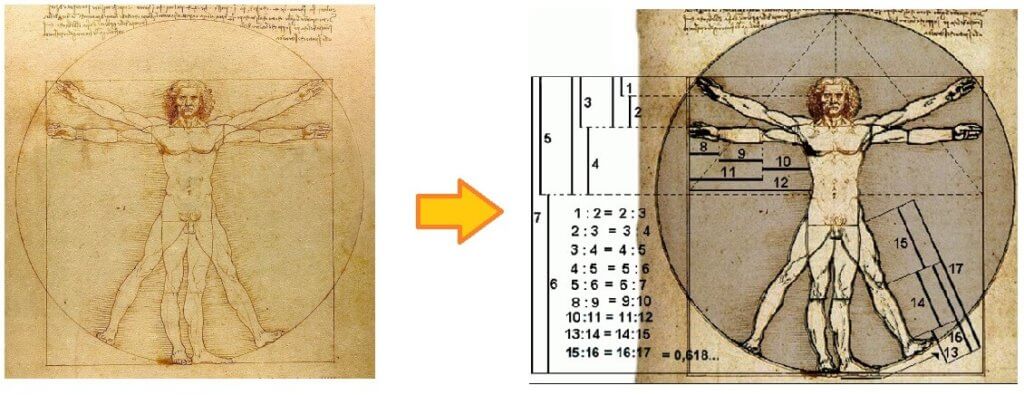
homem vitruviano leonardo da vinci razão áurea número de ouro

Para que você possa conferir as marcações e ver se de fato o número de ouro está presente no desenho, deixo aqui uma atividade interativa pra você testar no computador (no celular e, principalmente, no tablet não dá pra interagir legal, tá?). Mova o segmento, dividido em média e extrema razão, para cima do Homem Vitruviano e veja se encontra alguma coisa aí.

Ah, com uma trena ou uma régua, você pode fazer esse teste em casa também, usando o próprio corpo. Por exemplo, meça sua altura e a distância entre seu umbigo e o chão. Agora divida a medida maior pela menor e veja se o número de ouro aparece. Eu testei aqui comigo e não encontrei nada.

Contudo, como curiosidade, pra não dizer que o corpo não exibe proporções áureas, encontramos uma pesquisa, feita por Olivete e Evandro da Escola de Engenharia de São Carlos – USP, que mostrou que as falanges dos dedos de pacientes entre 6 a 15 anos apresentou a tendência à proporção áurea. Se quiser conferir, é só clicar aqui.

Outra coisa que é comum ouvir por aí sobre o número de ouro, é que podemos encontrá-lo na concha de Nautilus.

– Mas isso é verdade?

Olha, até podemos adotar a espiral áurea como um possível modelo para descrever a curva da concha de Nautilus. Inclusive, deixei uma atividade interativa com essa espiral para que você possa testar o encaixe da espiral com a curva da concha.

Espiral Áurea

Nada mal, né? Até que ficou interessante. Mas a pergunta que fica é: existe um modelo melhor para descrever a curva da concha de Nautilus?

Opa! Existe sim.

Olha aí embaixo uma espiral configurável que, apesar de não ser áurea, se encaixa muito bem. Se você quiser, pode mexer nos parâmetros para modificar a espiral.

Espiral logarítmica configurável

Vale ressaltar que o Mario Livio, autor do livro que citei anteriormente, afirma que a espiral áurea está presente na concha de Nautilus, no desenho das galáxias e tal.

Não sei você, mas (pra mim) a espiral logarítmica configurável se encaixou MUITO melhor na concha do que a espiral áurea. É tão perfeita que dá vontade de chorar. Mentira. ¬¬

Dá uma olhadinha no vídeo da BBC sobre a concha de Nautilus. Veja o número que eles encontraram.

Agora, como curiosidade, pra você que não sabe como se obtém uma espiral áurea, olhe o GIF a seguir.

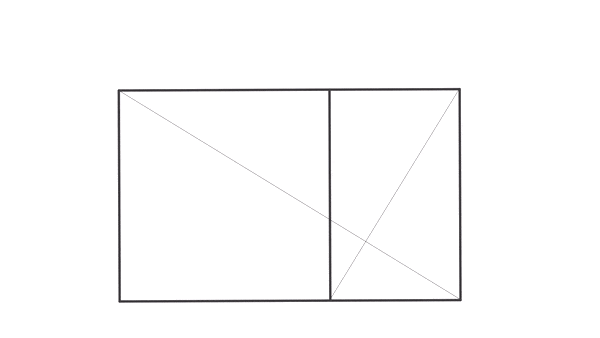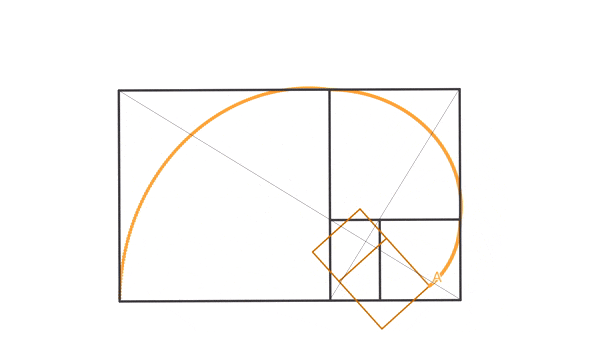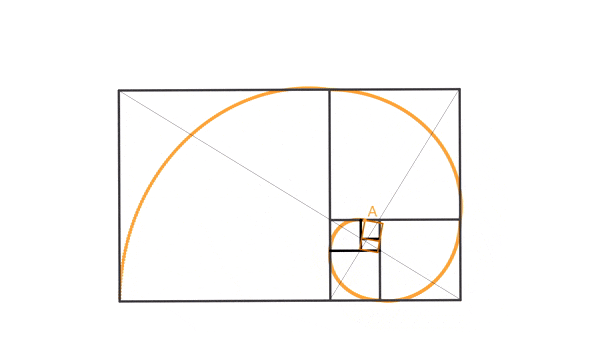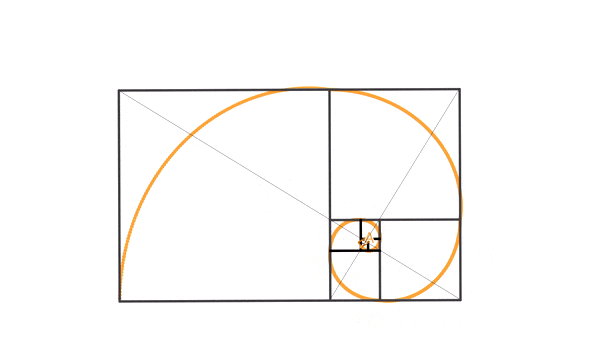
gif retângulo áureo espiral número de ouro

A expressão “seção áurea” (ou razão áurea) foi usada pela primeira vez pelo matemático alemão Martin Ohm (irmão do físico famoso Georg Simon Ohm) na 2ª edição do livro “A matemática elementar pura”, de 1835. Porém, não foi ele que inventou a expressão. E, no início do século XX, o matemático norte-americano Mark Barr atribuiu (equivocadamente, como vimos no vídeo Fake news sobre o número de ouro) a letra grega Fi em homenagem ao escultor grego Fídias, aquele do Partenon.

– Resumindo, o número de ouro é uma farsa?

Primeiro, não coloque a culpa no número, ele não tem nada a ver com isso. ¬¬

– Mas o que é verdade, então?

Podemos usar o número de ouro de forma indireta (por meio da Sequência de Fibonacci) para modelar o crescimento dos gomos de uma pinha, ou a curva das sementes do girassol etc. Vou deixar a Inês, do canal MathGurl, responder à sua pergunta. Na minha opinião, um dos canais mais divertidos do YoutTube que trata de Matemática. Óia aí.

E pra não dizer que não falei de música, vou citar um caso que envolve os violinos Stradivarius.

Algumas pessoas ~~malucas~~ divulgam por aí que os violinos Stradivarius, conhecido por muitos músicos como os melhores violinos do planeta, têm o som perfeito porque possuem a razão áurea. Será verdade mesmo?

Pra começar, apesar de ser um instrumento maravilhoso e objeto de desejo de muitos violinistas, depois de um teste cego, músicos profissionais não conseguiram distinguir um Stradivarius de um violino moderno de primeira linha. Se não acredita, clique aqui.

Vale destacar também que Antonio Stradivari tinha um cuidado especial em distribuir geometricamente o lugar dos buracos na em forma da letra f, em posições determinadas pela razão áurea.

Contudo, usar como argumento de que o som dele é perfeito apenas por causa da razão áurea e ignorar todos outros fatores como o verniz, o aferidor, a madeira etc. é um pouco desonesto, na minha opinião. Enfim…

Bem, chega por hoje, né? Agora que você já sabe bastante coisa sobre o número de ouro, que tal aplicar o que você aprendeu na tirinha do começo do post? Escolha qualquer quadro da tirinha, meça com uma régua o lado maior e anote o valor. Depois, meça o lado menor e anote também. Agora, divida a medida do lado maior pela medida do lado menor. E aí, o que você encontrou?

Só uma dica: eu fiz os quadros da tirinha usando um retângulo áureo de propósito, claro. 😉