
Bora ouvir um podcast sobre a origem do xadrez? =)
Se quiser saber um pouco mais sobre o xadrez, assista ao vídeo a seguir.
Agora, chegou a hora de encarar a parte matemática do negócio. Para isso, vamos analisar um trecho do livro de Malba Tahan, “O homem que calculava”. Se liga!
De acordo com um trecho do livro, o criador do xadrez recebeu por sua brilhante invenção o direito a um pedido do rei:
– Quero recompensar-te, meu amigo, por este maravilhoso presente, que de tanto me serviu para alívio de velhas angústias. Dize-me, pois, o que desejas, para que eu possa, mais uma vez, demonstrar o quanto sou grato àqueles que se mostram dignos de recompensa. “
E o inventor pediu:
– Dar-me-eis um grão de trigo pela primeira casa do tabuleiro; dois pela segunda, quatro pela terceira, oito pela quarta, e, assim dobrando sucessivamente, até a sexagésima quarta e última casa do tabuleiro. Peço-vos, ó rei, de acordo com a vossa magnânima oferta, que autorizeis o pagamento em grãos de trigo, e assim como indiquei!
E aí, leitor, essa quantidade de grãos cabe em suas mãos? E num caminhão? E em duas piscinas olímpicas? Difícil de responder? Nossa intuição, às vezes, pode nos enganar.
Para encontrar a quantidade de grãos de trigo, você deve somar os termos da seguinte sequência: 1, 2, 4, 8, 16, 32… até o último termo que é 2 elevado a 63.
Complicado?
Com uma fórmula Matemática e uma calculadora você consegue calcular isso.
Sn : Soma da PG.
a1 : primeiro termo da soma, no caso, o número 1.
q : é a razão da PG. Cada termo da soma, a partir do segundo, é obtido multiplicando-se o anterior por uma constante q, que neste caso, é o número 2.
n : número de termos da soma.
Faça um teste simples:
Se você não possui uma calculadora científica, clique aqui, encontre o resultado de 2 elevado a 63, que é apenas uma parcela da soma, e compare com este valor 18.446.744.073.709.551.615, que é o número total de grãos de trigo que o criador do xadrez receberia pela invenção.
>>Fato! Para preencher toda superfície terrestre (510.100.000 km2) com essa quantidade de grãos, teríamos aproximadamente 36 mil grãos por centímetro quadrado. Imagine empilhar 36 mil grãos em cada quadradinho. Incrível, não é?
Gostou de saber um pouco sobre esse jogo milenar? Que tal aprender as regras e jogar um pouco?

Fonte: Portal do professor (MEC), UOL educação, Site E-cálculo, Ciência à mão, livro ‘O homem que calculava’ de Malba Tahan e o livro Matemática, construção e significado.
►Para saber mais:
- A origem do jogo xadrez;
- Malba Tahan;
- Calculadora online;
- A história do xadrez;
- Intuição matemática, Maria Ângela de Carvalho;
- Progressões geométricas;
- Canal do Krikor, GM brasileiro;
- Canal do Rafael Leitão; GM Brasileiro;
- Canal do Evandro Barbosa, GM Brasileiro;
- Canal do Rafael Leite, Divulgador de Xadrez;
Acesso em 05 de Janeiro de 2019.


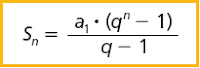




Comentários